Interest = Amount - Principal

Let Principal = P, Rate = R% per annum, Time = n years.

When interest is compound Annually:

Amount = P		1 +	R		n
			100

When interest is compounded Half-yearly:

Amount = P		1 +	(R/2)		2n
			100

When interest is compounded Quarterly:

Amount = P		1 +	(R/4)		4n
			100

When interest is compounded Annually but time is in fraction, say 3 years.

Amount = P		1 +	R		3	x	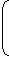	1 +	R
			100						100

When Rates are different for different years, say R₁%, R₂%, R₃% for 1^st, 2^nd and 3^rd year respectively.

Then, Amount = P

1 +

R1

1 +

R2

1 +

R3

.

100

100

100

Present worth of Rs. x due n years hence is given by:

Present Worth =	x	.
	1 + R 100